HMO-plus version 2.0
Written by Allan Wissner
Since the
original description of HMO 1.1 was published [Wissner, A. Tetrahedron Computer
Methodology. 1990, 3, 63-71], a number of modifications and
improvements have been made; these are described herein. The current version of
the program is HMO-plus 2.0
Changes to HMO-plus version 2.0
1. The program will now display a graphic representation of the
molecular orbitals that are constructed using Slater type atomic orbitals
(STOs) [J. C. Slater, Phys. Rev., 1930, 36, 57 ; K. B. Wiberg,
"Physical Organic Chemistry", Wiley, 1964, pgs 25-26, 469-471]. Normalized STOs
for 2pz and 3pz valence orbitals have the form:
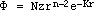
where N and K are constants that depend on the particular element and are
calculated using simple rules derived by Slater. The constant N also includes
the normalization factors. For a point in space, r is the distance of nucleus
to this point and z is the distance of the point along the axis of the pz
orbital; n is the principle quantum number; for the atoms supported by the
program, n has the value 2 or 3.
The actual STO formulas used are listed in Table I. All elements for which
default parameters have previously been provided are supported with an STO. For
user defined atom types, the program will attempt to use the most appropriate
STO formula otherwise the STO for carbon will be used. Distances used with
these STO equations are expressed in angstroms.
Table I. Normalized STOs for distances in angstroms.
| atom | type | STO
|
|---|
| C | 2pz | 3.590 ze-3.070
|
| O | 2pz | 8.326 ze-4.300
|
| N. | 2pz | 5.663 ze-3.686
|
| B | 2pz | 2.055 ze-2.458
|
| O: (O+) | 2pz | 10.020 ze-4.631
|
| N: (N+) | 2pz | 7.020 ze-4.017
|
| F | 2pz | 11.625 ze-4.915
|
| S: (S+) | 3Pz | 7.397 zre-3.655
|
| S. | 3pz | 5.953 zre-3.434
|
| Cl | 3pz | 8.825 zre-3.844
|
| P. | 3pz | 3.814 zre-3.025
|
| P: (P+) | 3pz | 4.880 zre-3.245
|
| Si | 3pz | 2.290 zre-2.614
|
The MO wave functions have the familiar LCAO form:
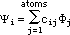
which after substituting the STOs becomes:
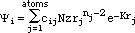
This equation is used to build the ¼-MO diagrams. In constructing the
diagrams, it is assumed that the molecule is planar. The screen coordinates are
converted to cartesian coordinates by first finding the average bond length of
the molecule in screen coordinates and then equating this average to 1.40
Å.
Attempts to use the above equation in analytic form to calculate the ¼-MO
diagrams proved to be extremely slow on a MAC IIci, even to the extent that the
calculation was not practical. This problem results from the large number of
exponential terms that have to be evaluated at each region of space. In order
to address this, the STOs are pre-calculated for distances up to 6.0 Å in
units of 0.01 Å.; the resulting numeral data is then stored in the
program and is retrieved from a look-up table as needed to generate the
diagrams.
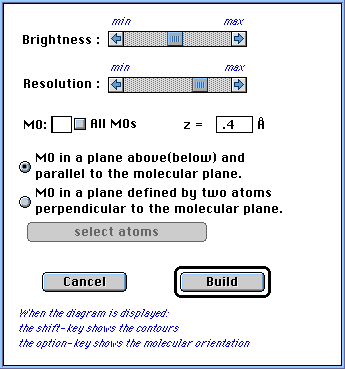
¼-MO diagrams are constructed by the program that show a view of the MO in
a plane located above or below and parallel to the molecular plane. The user
can specify the distance of the plane along the z axis (positive z is above and
negative z is below the plane); the default value of 0.4 Å is usually a
good choice and is close where the wave function has a maximum values (see
dialog box below).
A diagram can also be constructed that shows a view of the MO in a plane that
is defined by any two atoms and is perpendicular to the molecular plane. The
defining atoms can be chosen graphically by using the "select atoms" button
(see dialog box below). Because the orientation of the molecule will change
when this type of diagram is created, the orientation of the molecule and the
relative placement of the plane can be visualized by holding down the option
key. A scale, calibrated in angstroms, will also appear. In fact, this type of
diagram is not restricted to a plane defined by two atoms of the molecule. By
making use of dummy atoms, any plane perpendicular to the molecular plane can
be used. In order to define this plane, activate the structure window
after a calculation has been completed. Draw a new bond which will be
used to define the plane; the dummy atoms created by this bond can be chosen as
the atoms which define the plane. In doing so, they will not effect the diagram
in any other way.
In both types of diagrams, a positive value for the wave function is colored
blue while a negative value is colored red. The brightness of the color in a
given region is proportional to the magnitude of the wave function in that
region. Pure black would indicate that the function has a zero value.
HMO-plus will also perform a population analysis of the ¼-electronic
distribution. For a point in space, the ¼-electron density is given by:
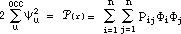
where again we use normalized STOs for the atomic orbitals
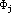 and the factors, Pij, are elements of the bond order - electron density matrix.
The summations in the right-hand formula are over all atomic orbitals. This
equation can be expanded to give:
and the factors, Pij, are elements of the bond order - electron density matrix.
The summations in the right-hand formula are over all atomic orbitals. This
equation can be expanded to give:
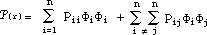
The first term in the expanded formula represents contribution of the atom
centered population to the total ¼-electron density while the second term
gives the bond centered population. HMO-plus will provide diagrams for the
total ¼-electron density distribution as well as separate diagrams for the
atom centered and bond centered distributions.
These diagrams depict a view of the ¼-electron density in a plane located
above or below and parallel to the molecular plane. The user can specify the
distance of the plane along the z axis. The electron cloud is shown in blue
where the brightness of the color is proportional to the magnitude of the
electron density in that region.
A ¼-electron density difference map can be constructed based on the formula
:
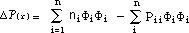
This map is a graphical representation of the difference between the molecular
atom-centered population and the ¼-electron density in the corresponding
isolated atoms placed at those positions which they occupy in the molecule. The
resulting diagram is a pictorial representation of the charge density within
the molecule. A negative density will be shown in red and a positive density in
blue. In the above formula ni is the number of electrons contributed to the
¼-system by atom i.
Before any of these diagrams are created, the user is presented with a dialog
box containing scrolls bars that control the overall brightness and the
resolution of the diagrams. The default setting for brightness is usually
sufficient. The brightness control has no effect on the speed of creation of
the diagram. With respect to the resolution of the diagrams, there is a
significant time penalty for the higher resolution settings.
For any of the above types of diagrams, the ¼-MO or electron density
contours can be displayed by holding down the shift key; these contours are
displayed as a series of randomly color bands where the width of a band is a
measure of the rate of change of the wave function or electron density,
respectively, in the region of space considered. In addition, with any of the
above diagrams, when the cursor is placed within the window containing the
diagram and the mouse button is held down, the numeral value of the wave
function or electron density at the point indicated by the cursor will be
displayed until the button is released.
These diagrams require systems operating with 32bit Quickdraw and best results
are obtained when 256 colors are chosen from the Monitors control panel. As is
the case with all the graphics generated with HMO-plus, these diagrams can be
printed (in color or B&W), saved as PICT files, or copied to the clipboard.
About 30K of ram is needed for each color diagram held in memory; in addition,
a 500K off screen buffer is temporarily allocated for construction of the
diagrams. Because of these memory requirements, no color diagrams can be
constructed when the program is configured to run at the recommended minimum
memory setting. If possible, the program should be operated at the preferred
setting or greater (the memory requirements of the program can be changed by
choosing "Get Info" from within Finder).
2. HMO-plus will now execute self-consistent field (SCF) calculations
using what is commonly referred to as the Pariser-Parr-Pople approximation
(PPP-SCF) [R. Pariser, R.G. Parr, J. Chem. Phys., 1953, 21, 466, 767;
J.A. Pople, Trans. Faraday, Soc., 1953, 49, 1375]. The PPP-SCF
calculations, as implemented in HMO-plus, are for closed shell systems only
without configuration interaction (CI). A full discussion of PPP-SCF theory
will be avoided here although the parameterization scheme used will be
addressed; the user is referred to the following discussions of PPP-SCF theory
: R.L. Flurry,Jr., "Molecular Orbital Theories of Bonding in Organic
Chemistry", Marcel Dekker, Inc., New York, 1968; L. Salem, "The Molecular
Orbital Theory of Conjugated Systems", W.A. Benjamin, Inc., New York, 1966;
M.J.S. Dewar, "The Molecular Orbital Theory of Organic Chemistry", McGraw Hill,
Inc., New York, 1969.
As implemented by HMO-plus the diagonal elements (Fii) of the Fock matrix are
given by:
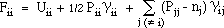
The off-diagonal matrix elements (Fij) are given by:
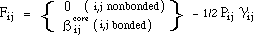 where Pij are elements of the bond order - electron density matrix, nj is the
number of electrons contributed to the ¼-system by atom j,
where Pij are elements of the bond order - electron density matrix, nj is the
number of electrons contributed to the ¼-system by atom j,
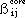 are the core resonance integrals,
are the core resonance integrals,
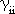 are the one-center electron repulsion integrals, and
are the one-center electron repulsion integrals, and
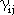 are the two-center electron repulsion integrals.
are the two-center electron repulsion integrals.
The usual assumption is made that the coulomb integral parameter, Uii, can be
equated with the negative of the valence state ionization potential (VSIP) of
atom i and that the one-center electron repulsion integrals,
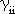 are given by the difference between the ionization potential and electron
affinity of atom i. The valence state data of Hinze and Jaffe are used to
evaluate these quantities [J. Hinze, H.H. Jaffe, J. Amer. Chem. Soc., 1962, 84,
540]. These data can be edited by choosing an atom from the palette while the
command-key is held down and then pressing the button "SCF-PPP"; the
valence state data for the atom will then be available to the user for
modification. Radio buttons are presented that allow switching the data display
for atoms that contribute one or two electrons to the ¼-system.
are given by the difference between the ionization potential and electron
affinity of atom i. The valence state data of Hinze and Jaffe are used to
evaluate these quantities [J. Hinze, H.H. Jaffe, J. Amer. Chem. Soc., 1962, 84,
540]. These data can be edited by choosing an atom from the palette while the
command-key is held down and then pressing the button "SCF-PPP"; the
valence state data for the atom will then be available to the user for
modification. Radio buttons are presented that allow switching the data display
for atoms that contribute one or two electrons to the ¼-system.
As pointed out by Sane and Sane (K. Sane, K. V. Sane, Indian J. Chem., Sect.
A 1977 , 15A(8), 740.), equating Uii with the negative of the VSIP of an atom
is a valid approximation only if the atomic orbital belongs to a non-orthogonal
basis set. Since the an orthogonal basis set is assumed in the PPP method, a
correction to the coulomb integral parameter is needed. Such a correction can
optionally be incorporated into the parameterization scheme by activating the
check box "Use Sane correction". Uii will then be given by:
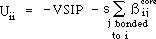
where s can be considered as the overlap integral but is used here as a
constant parameter that is adjusted to give best agreement between the
calculated and experimental ionization potentials. Correcting the coulomb
integral parameter in this manner results in far improved predictions of
ionization potentials (see below).
The two-center electron repulsion integrals can be evaluated either with the
formula of Beveridge and Hinze [ D.L. Beveridge, J. Hinze, J. Amer. Chem Soc.,
1971, 93, 3107] or the formula of Nishimoto and Mataga [K. Nishimoto, N.
Mataga, Z. Physik. Chem. (Frankfurt), 1957, 12, 335]. When performing a PPP-SCF
calculation the user is presented with the option of choosing one or the other
of these two formulas. With consideration of the other parameters used in this
implementation and the lack of CI, it appears that use of the later formula
gives better predictions of the ionization potential of molecules than the
former (although these predictions are routinely too high unless the correction
is applied to the coulomb integral parameter).
The formula for evaluating the core resonance integrals, 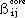 is given by :
is given by :
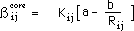
where
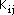 is the resonance integral parameter for atoms i and j that is used in the
Hückel calculations and
is the resonance integral parameter for atoms i and j that is used in the
Hückel calculations and
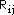 is the bond length between atom i and j. The quantities a and b are empirical
parameters. By using the bond lengths for ethylene and benzene along with the
respective empirical values for the core resonance integrals, the values a =
0.988 and b = 4.62 are found. The parameters a and b appearing in the above
formula can be changed by the user by choosing the menu item "ß-core
Integral Formula..." from the "Parameters" menu. The resonance
integral parameters,
is the bond length between atom i and j. The quantities a and b are empirical
parameters. By using the bond lengths for ethylene and benzene along with the
respective empirical values for the core resonance integrals, the values a =
0.988 and b = 4.62 are found. The parameters a and b appearing in the above
formula can be changed by the user by choosing the menu item "ß-core
Integral Formula..." from the "Parameters" menu. The resonance
integral parameters,
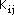 were original derived employing PPP-SCF calculations [F. A. Van-Catledge, J.
Org. Chem., 1980, 45, 4801] that use the Beveridge and Hinze [ D.L. Beveridge,
J. Hinze, J. Amer. Chem Soc., 1971, 93, 3107] parameterization scheme which in
turn uses the Ohno formula [K. Ohno, Theoret. Chim. Acta, 1964, 2, 219] for
evaluating the core resonance integrals. Thus, the above formula for
were original derived employing PPP-SCF calculations [F. A. Van-Catledge, J.
Org. Chem., 1980, 45, 4801] that use the Beveridge and Hinze [ D.L. Beveridge,
J. Hinze, J. Amer. Chem Soc., 1971, 93, 3107] parameterization scheme which in
turn uses the Ohno formula [K. Ohno, Theoret. Chim. Acta, 1964, 2, 219] for
evaluating the core resonance integrals. Thus, the above formula for
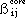 used by this program has the same 1/R dependence as the Ohno formula from which
the
used by this program has the same 1/R dependence as the Ohno formula from which
the
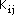 parameters were originally derived. By using this scheme to estimate the core
resonance integrals, no additional parameters other than a and b had to be
incorporated into the program.
parameters were originally derived. By using this scheme to estimate the core
resonance integrals, no additional parameters other than a and b had to be
incorporated into the program.
Unlike a simple Hückel calculation where the results depend only on the
connectivity within the molecule and not its actual geometry, a SCF-PPP
calculation requires input of atom-atom distances in order to determine the
appropriate values for the various integrals. HMO-plus has been designed to
make input of the molecular geometry fairly transparent to the user. The
molecule, as drawn by the user, is considered to be planar. It is assumed that
a linear relationship exists between the ¼-bond order and bond lengths of
the form:
Rij = k - hPij
where k and h are constants which depend on the atoms i and j. For the
different types of hetero- and homo-nuclear bonds, a series of k and h values
have been extracted from the literature or estimated from tables of standard
bond lengths and incorporated as parameters to the program [(a) M.S. Dewar,
G.J. Giecher, J. Amer. Chem. Soc., 1965, 87, 685. (b) I. Fisher-Hjalmars, S.
Meza; Acta Chem. Scand.,1972, 26 ,2991. (c) A. Skancke, P.N. Skancke, Acta
Chem. Scand., 1970, 24, 23. (d) G. Hojer, S. Meza, M.E. Ruiz, Acta Chem.
Scand., 1974, 27,1863. (e) O. Gropen, P.N. Skancke, Acta Chem. Scand., 1970,
24, 1768. (f) W.J. Hehre et al J. Chem. Phys.,1970, 52, 2769]. The button
entitled "Bond order-bond length equations..." located in the parameters
window will allow the user to modify existing h and k values or add values for
bond types that are not currently defined. From the initial ¼-bond orders
obtained from the beginning Hückel calculation, the bond lengths can be
calculated using these linear relationships; these lengths are then used, in
turn, to derive the core resonance integrals and the two-center electron
repulsion integrals. During each cycle of iteration, the bond lengths are
recalculated from the new bond orders and these are used to reevaluated the
integrals. The resulting calculation then is self-consistent for the variations
of the integrals with bond length. This scheme for allowance of molecular
geometry in hydrocarbons was previously adapted by Dewar and Giecher [M.S.
Dewar, G.J. Giecher, J. Amer. Chem. Soc., 1965, 87, 685]. While the above
scheme is useful for distances between bonded atoms, the longer range distances
are evaluated using the geometry as drawn by the user and are not reevaluated
for each iteration. To do this the screen coordinates must be calibrated to
correspond to the cartesian coordinates; this is done by first finding the
average bond length of the molecule in screen coordinates and then equating
this average to 1.40 Å. It is therefore important to draw structures
that, as far as possible, have equal bond lengths and reasonable bond angles so
as to accurately depict these long range interactions.
Calculations can also be executed using a defined geometry such as the
experimental geometry. This is accomplished by making use of the user defined
atoms that are accessed using the
tool of the palette. Atoms can be defined such that k is equal to the actual
bond length and h = 0 so that there would be no bond order dependence of the
bond length. A sample HMO-plus document illustrating this is provided.
Although many aspects of the parameterization scheme implemented herein have
been used before, the combination of these aspects are, in some ways, unique.
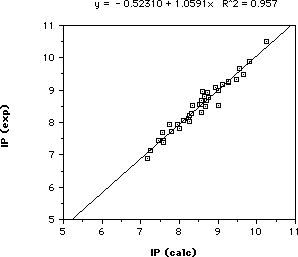
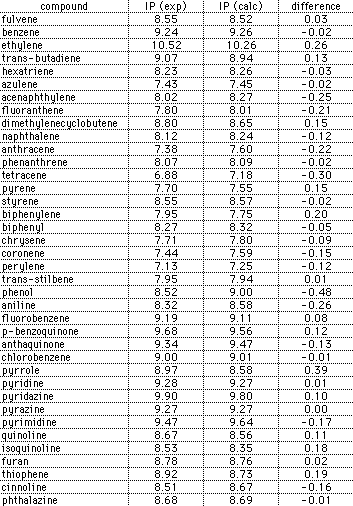
In order to validate this parameterization scheme, a comparision of the
calculated and experimental first ionization potentials has been made for a
variety of hydrocarbons and heteroatom-containing molecules. The results of
this comparison are shown in the graph and table below:
Changes to HMO-plus version 1.5-1.7
1. The name of the program has been changed slightly to HMO-plus
in an attempt to distinguish it from at least two other programs (one
shareware and the other commercial) called HMO; the "plus" designation is an
indication that this program does more than just simple Hückel
calculations.
2. The program now calculates and displays a ¼-electrostatic
potential diagram. A simple point charge model is used. At any point in space,
the ¼-electrostatic potential is the potential energy resulting from the
force exerted on a unit positive charge by the ¼-electron charge of each
atom of the molecule. In calculating the potential, it is assumed that the
molecule is planar and that the charges are located at points corresponding to
the atomic coordinates; the potential is calculated within the plane of the
molecule by summing the contribution of each atomic charge to the potential
energy (at any given point in space: ¼-electrostatic potential = Σ
qi/di where the qi is the ¼-charge and di is the distance of atom
i to that point ).
A positive potential is colored blue and a negative potential is colored red.
The brightness of the colors are proportional to the magnitude of the
potential. Pure black would indicate a zero potential. When the
¼-electrostatic potential diagram is requested using the command located
under the Diagrams menu, the user is presented with a dialog box containing
scrolls bars that control the overall brightness and the resolution of the
diagram. The default setting for brightness is usually sufficient; it may have
to be decreased for molecules bearing full charges or increased for molecules
with charges of low magnitude. The brightness control has no effect on the
speed of creation of the diagram. In setting the resolution of the diagram,
there is a significant time penalty for the highest resolution setting.
While the option key is held down and the ¼-electrostatic potential diagram
is located in the front window, the direction and magnitude of the ¼-dipole
moment will also be displayed.
While the shift key is held down and the ¼-electrostatic potential diagram
is located in the front window, the electrostatic potential contours will be
displayed as a series of randomly color bands where the width of a band is a
measure of the rate of change of the potential in the region of space
considered.
This diagram requires systems operating with 32bit Quickdraw and best results
are obtained when 256 colors are chosen from the Monitors control panel.
Changes to HMO version 1.4
1. The energy level diagrams generated with previous versions of
HMO were restricted to the range +/- 3ß. Version 1.4 removes this
restriction. To see energy levels outside the range +/- 3ß, place the
cursor within the energy level window and drag up or down while holding the
mouse button down; the energy level diagram will then scroll vertically.
2. The energy level diagram of previous versions of the program only
displayed degenerate energy levels up to 3. Version 1.4 will show all the
degenerate energy levels present.
3. In order to do calculations on Mobius systems, negative resonance
integrals have to be used. Earlier versions of the program would not accept a
negative value for a resonance integral. This has been corrected in version
1.4
4. A "Check valences" item has been added to the "Structure" menu. You
can now turn valence checking on or off. This is useful if you frequently do
calculations on certain polyhedra where the number of bonds attached to a node
can exceed the normal valence of carbon.
5. Two items have been added to the "Structure" menu: "Read connection
table" and "Write connection table". Structures can now be imported and
exported to ChemDraw(TM) via connection tables.
6. A horizontal scroll bar has been added to the eigenvalue diagram
window. This control now allows the size of the depicted electron densities to
be varied relative to the structure.
7. Previous versions of the program allowed the results of a
calculation to be saved either as text or as PICT documents; they did not allow
the user to save a calculation as a document that could later be opened and
viewed by the program HMO. This ability has now been added. The "File"
menu has been modified to accommodate this new functionality as follows:
Open Calculation...: This command opens a previously saved calculation
document.
Close Calculation: This command will close the currently displayed
calculation. If it is a new calculation, the user is prompted to save the
file.
Save Calculation...: The calculation is saved as a disk file.
Open Structure...: This command allows a previously saved structure
template to be loaded from a disk file and displayed in the "Structure"
window.
Close Front Window: The current active window is closed.
Save as... : The exact title of this menu item will depend on which
window is foremost. For example, when the "Structure" window foremost, the menu
item will read "Save Structure as..." ; the current structure will be saved as
a disk file which can later be opened by HMO. The tabular results are saved as
a text file and the various diagrams are saved as PICT files which can be
opened with a drawing program such as Macdraw.
Page Setup... : Gives the standard Macintosh page setup dialog. The
items in this dialog will determine how many of the diagrams can be fitted on a
page.
Print... : The contents of all windows open at the time this command is
chosen will be printed.
Quit: Exits the program. If a new calculation has been performed, the
user is prompted to save it as a disk file. The identical item in the palette
serves the same purpose.
8. The "Results" menu has been replaced by two new menus: The
menu labeled "Diagrams" has menu items that allow the display of several
types of diagrams of the calculation results. The new menu items include:
Charge density diagram... : A display of the ¼-charge densities is
presented where a negative charge is represented by an open circle and a
positive charge is represented by a filled circle. The diameter of a circle is
proportional to the magnitude of the charge density. The horizontal scroll bar
allows the diameter of the circles to be adjusted relative to the structure.
The charge density diagram also shows the magnitude and direction (relative to
the screen) of the ¼-dipole moment. The ¼-dipole moments calculated by
HMO are only approximate and depend on how the structure is displayed on the
screen. The following procedure is followed: The average distance separating
the bonded atoms of the screen representation of the structure is determined
and equated to 1.4 Å. All bond lengths are then assumed to be equal to
this average length. The dipole moment is then calculated as the vector sum of
the charge distribution using this assumed geometry.
Free valence diagram... : A display of the free valences is presented
where the diameter of a circle is proportional to the magnitude of the free
valence. The horizontal scroll bar allows the diameter of the circles to be
adjusted relative to the structure.
Superdelocalizability diagrams... : A display of the
superdelocalizabilities is presented where a negative superdelocalizability is
represented by an open circle and a positive superdelocalizability is
represented by a filled circle. The diameter of the circle is proportional to
the magnitude of the superdelocalizability. The vertical scroll bar alters the
display to show electrophilic, radical, and nucleophilic
superdelocalizabilities. The horizontal scroll bar allows the diameter of the
circles to be adjusted relative to the structure.
¼-Bond order diagram... : A display of the structure is presented
where the thickness of the bonds depends on the calculated ¼-bond order (the
relationship between thickness and bond order is not linear). The horizontal
scroll bar controls the resolution of the diagram. The vertical scroll bar
adjusts the contrast of the diagram.
Self-atom polarizability diagram... : A display of the self-atom
polarizabilities is presented where the diameter of a circle is proportional to
the magnitude of the polarizability. The self-atom polarizabilities are always
positive (actually, they are in units of 1/ß and ß is negative) and
are an indication of the magnitude of the change in charge that will be induced
at a given atom as a result of a change in the coulomb integral
(electronegativity) of that atom. The horizontal scroll bar allows the diameter
of the circles to be adjusted relative to the structure. Insofar as, a charged
reagent approaching an atom of a conjugated molecule induces a change in the
¼-electron distribution of that molecule, one might expect the self-atom
polarizabilitiy to be a measure of the reactivity of the various positions
within the molecule during the early transition state. The greater the
polarizabilitiy of an atom, the greater the reactivity at that
position.
Mutual-atom polarizability diagrams... : Mutual-atom polarizabilities
denote the change in charge that will be induced at other atoms of the
structure as a result of a perturbation of the coulomb integral of a given
atom. The diameter of a circle is proportional to the magnitude of the
polarizability; a negative polarizability is represented by an open circle and
a positive polarizability is represented by a filled circle. The largest
positive polarizability (filled circle) will be located on the perturbed atom
and it's diameter is proportional to the self-atom polarizability of that atom.
A negative mutual-atom polarizability (open circle) indicates that the change
in charge induced at that atom is opposite to that induced at the atom
undergoing perturbation. The vertical scroll bar alters the display to show the
polarizabilities as the perturbed atom is changed. The horizontal scroll bar
allows the diameter of the circles to be adjusted relative to the structure.
Placing the cursor within the circles contained in any of the above diagrams
will display the corresponding numeral values.
The menu entitled "Labels" has menu items that were previously located
in the "Results" menu.
9. The "Edit" menu is now fully supported; all text and
graphics can be copied to the clipboard and thereby exported any other program
that will except text or PICT graphics.
10. The number of undefined atom types for which the user can assign
resonance and coulomb integral parameters has been increase from three to
eighteen. They are now accessed utilizing the palette tool
 that activates a pop-up menu of undefined atoms.
that activates a pop-up menu of undefined atoms.
11. In addition to simple Hückel calculations, HMO 1.4 now allows
calculations to be executed using the ω-technique. The ω-technique
calculations are implemented as described by Wheland and Mann [ Wheland, G. W.;
Mann D. E., J. Chem. Phys., 1949, 17, 264. See also:
Streitwieser, A. J. Am. Chem. Soc., 1960, 82, 4123.]. The program
employs the modification suggested by Ettinger that results in a more rapid
convergence to a self-consistent charge distribution [Ettinger, R. Tetrahedron,
1964, 20, 1579]. After a structure is created and the user
presses the "Calculate" tool in the palette, the dialog box shown below will
appear containing the expected number of ¼-electrons and check boxes with
which the user indicates the desired output. Radio buttons are provided to
select the calculation type. If a simple Hückel calculation is to be
executed, the ¼-electron count is the only parameter needed. For
ω-technique calculations, the user must supply the maximum number of
iterations the program will perform before terminating the calculation (most
calculations will reach self-consistency before 15 iterations), the criterion
for a self-consistent charge distribution (usually 0.001 units), and the value
of the parameter ω (omega, usually 1.4).
In addition, when executing an ω-technique calculation, the option is
provided to have the off-diagonal matrix elements, corresponding to the bonded
atoms, calculated from the bond orders using an iterative procedure that
results in a final Hückel matrix that is self-consistent with respect to
both the diagonal and off-diagonal matrix elements. The method of Boyd and
Singer [Boyd, G, V.; Singer, N., Tetrahedron, 1966, 22, 3383] is
used to arrive at the off-diagonal elements that makes use of an empirical
relationship between the resonance integral ßrs for bonded carbon atoms r
and s and the bond order prs calculated for that bond: ßrs = ß0
exp(0.55prs - 0.3666); a new menu command, "Resonance integral-bond order
equation...", has been added to the Parameters menu that will allow the
user to change the parameters of this formula. Bond orders (prs) calculated
during one cycle are used to derive the resonance integrals (ßrs) that
are used in the next iterative cycle; the process is continued until the
derived matrix elements don't change by a specified amount. In the current
implementation, it was found that both the diagonal and off-diagonal elements
could be optimized together within the same iterative cycle.
Boyd and Singer also describe an empirical relationship between bond length
and bond order that has been incorporated into the program HMO. The relation,
Rrs = 1.524-0.194prs where Rrs is the bond length between atoms r and s and prs
is the bond order, gives good predictions of the bond lengths in alternate
hydrocarbons; a new menu command, "Bond length-bond order equation...",
has been added to the Parameters menu that will allow the user to change the
parameters of this equation.
A detailed description of the equations used in the ω-technique
calculation is located under the Apple menu.
For ω-technique calculations, a check box can be selected that allows a
separate text file to be created that contains the charge distributions and
bond orders calculated during each iteration; this information is useful in
situations where the calculation does not converge to a self-consistent charge
distribution. Pressing the "Calculate" button then begins the calculations (see
figure below).

12. HMO also executes what has been termed an Improved Two-parameter
Omega Technique calculation {ITPOT} [Mathur, S. C.; Singh, D. C.; Kumar, B.;
Mitra, S., Int. J. Quantum Chem., 1977, 11, 759 and Castro, E. A.;
Fernández, M., Z. Phys. Chemie, Leipzig, 1981, 262, 83.]. In this
technique, the diagonal matrix elements depend on the atomic orbital population
of an atom and its neighbors and the off-diagonal elements between bonded atoms
depend on the bond orders (using the same Boyd and Singer exponential
relationship described above for the simple ω-technique). In the
implementation used in HMO, we construct the secular determinant as described
by Castro with modifications to allow calculations for structures containing
heteroatoms. Since a careful analysis of the use of the default set of
heteroatom coulomb and resonance integral parameters with the parameters
ω and ω' has not been done, this technique should be used with
caution when applied to heterocyclic systems. The calculations are very
sensitive to the value of ω'. Originally, the parameters ω and
ω' were assigned the values 1.4 and -0.6, respectively; in a more recent
publication [Cachau, R.E.;Estiú, G.L.;Castro, E.A., Acta Chim. Sin.
1988, 46, 57], the values assigned were : ω = 1.7433 and ω' =
-0.495. Preliminary indications are that these new values give a better charge
distribution in heterocycles, nonalternate hydrocarbons, and ions than the
original values. A detailed description of the equations used in the ITPOT
calculations is located under the Apple menu.
13. Polarographic half-wave reduction potentials are calculated as
described by Fry and Fox [Fry, A.J.; Fox, P.C., Tetrahedron, 1986, 42, 5266].
The empirical equations described in the above reference are used for
calculating the reduction potentials when doing a Hückel or
ω-technique calculation. For ITPOT calculations, a linear equation [E1/2
= 2.82 x m<lumo> -0.0279, R = .98] was derived using a subset of the Fry
and Fox data with ω = 1.7433 and ω' = -0.495.
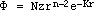
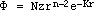
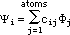
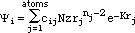

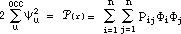
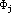 and the factors, Pij, are elements of the bond order - electron density matrix.
The summations in the right-hand formula are over all atomic orbitals. This
equation can be expanded to give:
and the factors, Pij, are elements of the bond order - electron density matrix.
The summations in the right-hand formula are over all atomic orbitals. This
equation can be expanded to give: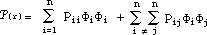
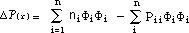
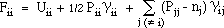
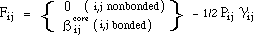
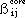 are the core resonance integrals,
are the core resonance integrals,
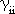 are the one-center electron repulsion integrals, and
are the one-center electron repulsion integrals, and
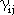 are the two-center electron repulsion integrals.
are the two-center electron repulsion integrals.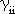 are given by the difference between the ionization potential and electron
affinity of atom i. The valence state data of Hinze and Jaffe are used to
evaluate these quantities [J. Hinze, H.H. Jaffe, J. Amer. Chem. Soc., 1962, 84,
540]. These data can be edited by choosing an atom from the palette while the
command-key is held down and then pressing the button "SCF-PPP"; the
valence state data for the atom will then be available to the user for
modification. Radio buttons are presented that allow switching the data display
for atoms that contribute one or two electrons to the ¼-system.
are given by the difference between the ionization potential and electron
affinity of atom i. The valence state data of Hinze and Jaffe are used to
evaluate these quantities [J. Hinze, H.H. Jaffe, J. Amer. Chem. Soc., 1962, 84,
540]. These data can be edited by choosing an atom from the palette while the
command-key is held down and then pressing the button "SCF-PPP"; the
valence state data for the atom will then be available to the user for
modification. Radio buttons are presented that allow switching the data display
for atoms that contribute one or two electrons to the ¼-system.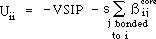
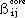 is given by :
is given by :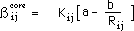
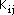 is the resonance integral parameter for atoms i and j that is used in the
Hückel calculations and
is the resonance integral parameter for atoms i and j that is used in the
Hückel calculations and
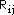 is the bond length between atom i and j. The quantities a and b are empirical
parameters. By using the bond lengths for ethylene and benzene along with the
respective empirical values for the core resonance integrals, the values a =
0.988 and b = 4.62 are found. The parameters a and b appearing in the above
formula can be changed by the user by choosing the menu item "ß-core
Integral Formula..." from the "Parameters" menu. The resonance
integral parameters,
is the bond length between atom i and j. The quantities a and b are empirical
parameters. By using the bond lengths for ethylene and benzene along with the
respective empirical values for the core resonance integrals, the values a =
0.988 and b = 4.62 are found. The parameters a and b appearing in the above
formula can be changed by the user by choosing the menu item "ß-core
Integral Formula..." from the "Parameters" menu. The resonance
integral parameters,
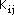 were original derived employing PPP-SCF calculations [F. A. Van-Catledge, J.
Org. Chem., 1980, 45, 4801] that use the Beveridge and Hinze [ D.L. Beveridge,
J. Hinze, J. Amer. Chem Soc., 1971, 93, 3107] parameterization scheme which in
turn uses the Ohno formula [K. Ohno, Theoret. Chim. Acta, 1964, 2, 219] for
evaluating the core resonance integrals. Thus, the above formula for
were original derived employing PPP-SCF calculations [F. A. Van-Catledge, J.
Org. Chem., 1980, 45, 4801] that use the Beveridge and Hinze [ D.L. Beveridge,
J. Hinze, J. Amer. Chem Soc., 1971, 93, 3107] parameterization scheme which in
turn uses the Ohno formula [K. Ohno, Theoret. Chim. Acta, 1964, 2, 219] for
evaluating the core resonance integrals. Thus, the above formula for
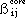 used by this program has the same 1/R dependence as the Ohno formula from which
the
used by this program has the same 1/R dependence as the Ohno formula from which
the
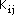 parameters were originally derived. By using this scheme to estimate the core
resonance integrals, no additional parameters other than a and b had to be
incorporated into the program.
parameters were originally derived. By using this scheme to estimate the core
resonance integrals, no additional parameters other than a and b had to be
incorporated into the program.