Orbital Diagrams for Simple Molecules

Instructions for Viewing

Ensure your browser has a 3D model plugin installed; Quick3D or 3DMFPlugin (both browser plugins), 3DMF Optimizer (a Macintosh application), Geo3D (for Mac) or 3DMF Viewer for Windows. Windows users must also install the QuickDraw3D libraries from Apple. To view a model, click on the picture of any model. A separate window will open containing the model.

Localised Orbitals in Methane and Cyclopropane

Note how the localised orbital in methane lies along the axis of the C-H bond, whereas the localised orbital in cyclopropane does not lie along the axis of the C-C bond, but is bent outside it (the banana shape, although in fact its more triangular than banana shape).
Localised C-H Orbital for Methane (3-21G* basis) Localised C-C Orbital for Cyclopropane (6-31G(d,p) basis)

The Bonding and Anti-bonding p Molecular Orbitals in Ethene and Cyclopropane

Ethen and cyclopropane are classified as alkene and alkane respectively, but the latter is often regarded as having properties associated with the former. These orbitals show why.
Ethene: Bonding Ethene:Anti-bonding Cyclopropane: bonding Cyclopropane: Anti-bonding
The pi orbital in ethene (3-21G*) The pi star orbital in ethene (3-21G*) The sigma /pi like orbital in cyclopropane 6-31G (d,p) The sigma /pi like antibonding orbital in cyclopropane 6-31G (d,p)

The Anti-bonding X-Y Molecular Orbital (LUMO) along the series XH3-Y

Nucleophilic attack on haloalkanes is often presented in terms of the highest occupied molecular orbital (HOMO) of the nucleophile interacting with the lowest unoccupied molecular orbital (LUMO) of the electrophile. This interaction is favoured both by good overlap between these two orbitals and by minimising the energy difference between them. To see how this works in practice, the table below shows the quantitative form and energies of the LUMO orbitals of the electrophile.

Various points are noteworthy. Thus although the LUMO of fluoromethane has the appropriate shape for an SN2 displacement by a nucleophile, its energy is very high and hence it does not interact at all favourably with the nucleophilic HOMO (F is rarely displaced in SN2 reactions). In contrast, the LUMO of iodomethane has an appropriate energy, but its shape has a higher density at the iodine end than the carbon end. Thus e.g. I- can attack at the iodine end under suitable circumstances. Finally, we note that whilst substitution at carbon electrophiles always goes with inversion, Silicon can substitute with retention of configuration, as the shape and energy of its LUMO in SiH3Fimplies.

Y X=Carbon X=Silicon X=Germanium X=Tin X=Lead
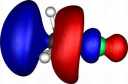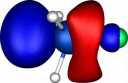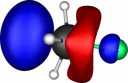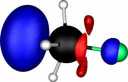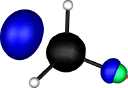Y=Fluorine The anti-bonding sigma star molecular orbital of fluoromethane The anti-bonding sigma star molecular orbital of fluorogsilane The anti-bonding sigma star molecular orbital of fluorogermylane The anti-bonding sigma star molecular orbital of fluorostannane The anti-bonding sigma star molecular orbital of fluoroplumbane
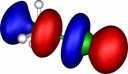Y=Chlorine The anti-bonding sigma star molecular orbital of chloroomethane The anti-bonding sigma star molecular orbital of chlorosilane
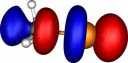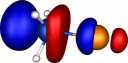Y=Bromine The anti-bonding sigma star molecular orbital of bromoomethane The anti-bonding sigma star molecular orbital of bromosilane
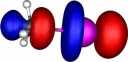Y=Iodine The anti-bonding sigma star molecular orbital of iodoomethane The anti-bonding sigma star molecular orbital of iodoomethane
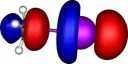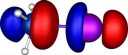Y=Astatine The anti-bonding sigma star molecular orbital of astatomethane The anti-bonding sigma star molecular orbital of astatoomethane

How were these orbitals produced?

Molecular Orbitals (MOs) are solutions of the Schroedinger equation for a molecule. Each MO has an associated eigenvalue (a discrete energy level) for an electron in a molecule, and is described by a set of coefficients (the wavefunction) expressed as a linear combination of the atomic orbital components of each atom in the molecule. The Hartree-Fock method is approximate way of solving the Schroedinger equation, a method implemented in a Quantum computational program called GAMESS. One particular representation of the atomic orbitals for each molecule is selected (called the basis set, in our case the 3-21G* basis) and the Hartree-Fock equations solved. An eigenvalue solution of these equations yields molecule orbitals (also often called canonical or delocalised orbitals), which are rendered visible by calculating the value of the wavefunction at any point in space and then contouring these values at one particular level (in our case 0.06 Atomic units) to create an "iso-surface" using a program called MacMolPlt. The result is written out into a 3D computer graphics file in 3DMF format, and displayed in a browser using a 3DMF plug-in. It is also possible to transform molecular canonical orbitals to a more localised form (an Edmiston-Ruedenberg transform) which are the ones shown above for methane and cyclopropane.