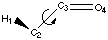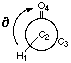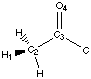
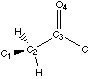
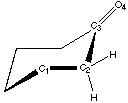
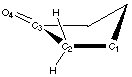
Structural dependencies of hydrogen bonds in methylcarbonyl and derived groups

  1. Introduction

    2. A broad and accurate defintion of the hydrogen bond has been given in 1960 by Pimentel and McClellan[20] :

    A H-Bond exists between a functional group A-H and an atom or a group of atoms B in the same or a different molecule when (a)there is evidence of bond formation (association or chelation), (b) there is evidence that this new bond linking A-H and B specifically involves the hydrogen atom already bonded to A

    We want to analyse hydrogen bonds with a proton on a carbon alpha to a carbonyl group or an other related group. The position of the proton is defined by a dihedral angle involving the carbonyl group (Figure 4.1). We want to compare calculations and experimental data. Calculations let us model the ease of creating hydrogen bonds as a property of the fragment (a partial charge on the proton). Experimental data shows the different dihedral angles for compounds in a database that contain such hydrogen bonds. We will first describe the method that can be used to measure the correlations, and then we will try to apply this method to the hydrogen bond we are are looking at.

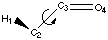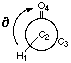Figure 4.1 : Definition of the Dihedral Angle

  1. Method

    2. The result of a search of the Cambridge Structural Database is a list of value for the parameter we are looking at (a dihedral angle).
Number of compounds = f  (parameter) (1)
    f  is a function that describes the repartition of the compounds that match the criteria of the search. We have to define the cutoffs of the interval in which the parameter may vary. There must be enough compounds in each sub-interval, and if there are too many, the cutoff can be refined. In our case the dihedral angle can vary between 0 and 180°. If we get enough hits in our search (more than twenty) we can divide this interval into 18 evenly sized parts.
    Then we have to compare these experimental data with the computed values. There is no single way to do it. The calculations enable us to compute a property which depends on the parameter. This property can, for example, be a partial charge or a heat of formation.
Property = g  (parameter) (2)
    We do not know how the number of compounds depends on the property, but we can try to guess it. We can simply have a linear dependence, or something more complicated like a Boltzmann function.
Number of compounds = h  (property) (3)
    h   belongs to a set of functions F which is not known. With (2) and (3), we have a new relation between the number of compounds and the parameter :
Number of compounds = h o  g  (parameter) (4)
    We will use a standard Khi2 test to measure the accuracy of the calculations and the pertinence of the model. With a simple optimization on the function h  belonging to F, we are now able to say if our sample fits the calculation or not.

  1. Carbonyl

    2. We want to know if there is a correlation between the hydrogen bond linking proton alpha to a carbonyl with another oxygen atom and the position of this proton. The position is characterized by the dihedral angle H-C-C=O. Numerical simulations enable us to calculate the partial charge on the hydrogen as a function of the dihedral angle (Graph 4.1).

    Several searches in a crystallographic database (the Cambridge Structural Database[27]) have been carried out. The requests specified that the distance between the hydrogen and the oxygen that form the hydrogen bond should be less than 2.3 Å (there is a Van de Waals contact when the distance is less than 2.6 Å, so we are sure that there will be a bond). Sheme 4.2 shows the results of this search.

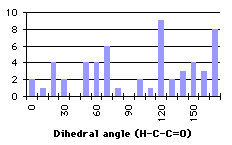Graph 4.2 : Number of compounds with hydrogen bond

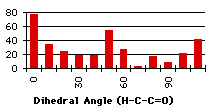
    At a first glance, we cannot find any correlation between the search and the partial charges. We wonder if we have to take into account the energy as a function of the dihedral angle to refine this analysis. Another source of apparent disorder in the results of the searches appears with the distinction between the different types (primary, secondary or tertiary) of the carbon holding the proton involved in the hydrogen bond. Unfortunately the shape of the graphs describing the energies and the partial charge on the proton as a function of the dihedral angle depends on the types of the carbon alpha to the carbonyl. We will make a review of the different kinds of groups, trying to correlate the dihedral angle distribution found in the database with the energies and the partial charge on the hydrogen.

    1. Heat of formation

    We have first studied the variations of the heat of formation. The dihedral angle was locked and the rest of the molecule was optimized. Results are given in Graph 4.3. Quaternary carbons were not taken into account because there are very few compounds in the database with this motif, and these compounds are often cyclic, which means that the dihedral angle is forced to certain values.
Primary
Secondary
tertiary

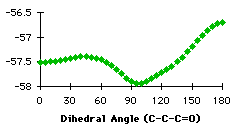
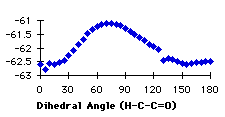
Graph 4.3

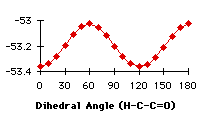
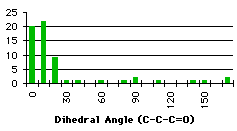
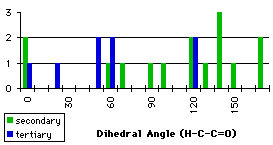
    The first atom of the dihedral angle in the second structure is a carbon, because it is smpler to describe the variation in this way. The minimum at 100° corresponds to two different dihedral angles for the hydrogens (-140° and -20°). We have the confirmation that we have to handle the different groups separately. We have searched the database for compounds containing the groups described in graph 4.3. In each case we specified that the atoms in the fragment may be linked to each other only by bonds given explicitly. This command (no links) avoided strained cycles.

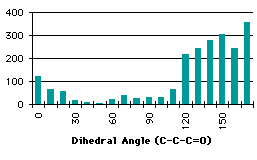Graph 4.4 : Number of compounds with secondary carbon

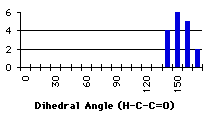
    The results for the group with a secondary carbon are opposite to those we expected. Most of the compounds have a dihedral angle between 120° and 180°. Examining some of these compounds, we observed that they contain five or six membered rings that force the dihedral angle  to be close to 120° or 180° (Figure 4.2)

6-members rings
 = ± 120°		 5-members rings
 = ± 180°

Figure 4.2 : Effects of rings on the dihedral angle 

    We have to reject the compound with these motifs. Therefore we use another command (no cyclic route) to specify that the selected atoms in the fragment may not be connected by a cyclic bond.

Primary
Secondary
tertiary

Graph 4.5

    When the utmost has been done to eliminate external causes of specificity in the repartition of the compounds, only a few molecules exhibit all the conditions to be good candidates to a repartition due only to energetic factors. Unfortunately, the synthetic results of the search (the repartition of the dihedral angles) do not have the same shape as the calculation results. At first glance, the correlation seems to be better with the primary carbon alpha to the carbonyl and we want to measure it. We will model a linear dependance of the number of compounds with the heats of formation (Graph 4.3). We will use eleven linear functions, with a simple principle of construction : the relative weights of the minimum and maximum heats of formation go from (1,0) to (1,1)*. This describes all the expected range of linear behaviours. Hereafter, the linear functions are multiplied by a coefficient that will give the same total number of compounds as we get from the search. The correlations found with the Khi2 are very small (<<10-10). To simulate exponential functions we made the same calculation with linear functions with respective weights for minimum and maximum going from (1,0) to (1,-1) and when the value of the function was negative, it was set to zero. Even in this case the correlations were very bad. The main problem is that the 'noise' is too important (the peak at 80° for instance) and there are probably some external factors that we have not taken into account (the large peak at 60°).

    1. Partial charges

    We follow the same procedure as has been described before, with a maximum distance between the oxygen and the proton forming the hydrogen bond of 2.3Å. Even without the 'no cyclic route' command, we did not get a lot of compounds. With tertiary carbons, we only get 8 compounds and with the secondary carbons, we get 15 compounds (Graph 4.6). There are not enough hits in the search to find any property.

Graph 4.6 : Number of compounds with hydrogen bond (secondary and tertiary carbons)

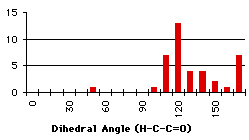
    With a methyl group (primary carbon alpha to the carbonyl), the search was extended to a maximum distance of 2.5Å. It is obvious that there are two main peak (graph 4.7). A detailed review of the compounds corresponding to these two peaks reveals that they belong to the same classes (Figure 4.3). The 120° peak correspond to a conjugated diketone where two hydrogens are forming a weak hydrogen bond: the oxygen-proton distance in the search result was between 2.3Å and 2.5Å. This other class of compound corresponds to a methyl ketone in a position ortho to an oxygen. The distance here is between1.8Å and 2.3Å.

Graph 4.7 : Number of compounds with hydrogen bond (primary carbons)

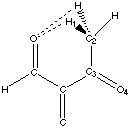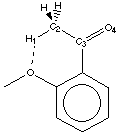Figure 4.3

  1. Other functional groups

    2. Other calculations have been carried out with different functional groups(Graph 4.1). Some of the corresponding searches in the Cambridge Structural Database have been made. With -NO2, we do not find any compound at all in the Database. For -OH and for the ester group -(CO2)-, the results are given in Graph 4.8 and 4.9. There seems to be no direct relation between the partial charges and the hydrogen bonds.

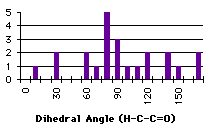Graph 4.8 : Number of compounds with hydrogen bond (Ester)

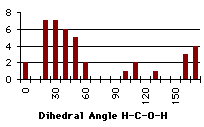Graph 4.9 : Number of compounds with hydrogen bond (alcohol)

  1. Conclusions

    2. This project could appear fruitless because of the lack of positive discovery. However there are a few ideas that could be born in mind. There are few intramolecular hydrogen bonds. If we were looking at strong bonds, we should only have kept the hydrogen bond shorter than 2.1Å and we would have only found very few compounds. To find intermolecular bonds, we should use other methods of searching.

    We could have searched the database to find compounds containing our fragment and an oxygen atom (or any other electronegative atom) without looking any geometrical property. Then we should have retrieved the shape of the crystal cell and carefully examined it to see if there is a hydrogen bound. This process implies that we have to write some programs to handle intermolecular hydrogen bonds.

    We are now aware of the different external factors that could occur in a statistical analysis on a chemical database. There are a lot of compounds but there are not so many different motifs. If our sample do not contain enough molecules, we may often encounter the same motifs and our analysis become meaningless.

    * The set of equations that defines the linear functions a(r).x+b(r) is :
a(r).H°min + b(r) = 1 (5)
a(r).H°max + b(r) = r (6)
r = 0, 0.1, 02, ... , 0.9, 1 (7)

Previous Table of Contents Next