Henry Rzepa's Blog

This is the time of year when I deliver two back-2-back lecture courses, and yes I do update and revise the content! I am always on the look-out for nice new examples that illustrate how concepts and patterns in chemistry can be joined up to tell a good story. My attention is currently on conformational analysis; and here is an interesting new story to tell about it.

Above is a seven-membered ring benzolactam[cite]10.1248/yakushi.13-00169[/cite]^‡, and it caught my eye because of the number of concepts (the semantic density if you like) contained in its chemistry.

1. The title contains the phrase amide-based axial chirality
2. and active
3. conformation
4. recognised by enzymes and receptors

All the above also implies:

1. chirality is associated with configurations, whilst conformation is associated with isomerism about single bonds
2. when conformational analysis is transplanted into a cyclic ring, it can morph magnificently into the land of configuration, via a process known as atropisomerism.
3. Amides themselves sit in the land between conformation and configuration. Pauling famously used this transition to help devise his helical structures for peptides by deducing that the apparent single N-C bond in an amide (= conformation?) is actually a partial double bond by resonance (= configuration).
4. The difference between a conformation and a configuration is simply kinetics. An approximate guideline is that if a particular pose in a system is prevented from exchanging with another pose by a half life of at least 1000 seconds, it is classified as a configuration, and if its half-life is less it is a conformation.
5. Of course enzymes and receptors recognise individual configurations, and hence respond differently. Again the vexed issue of lifetime rears its head. Thus the configuration of thalidomide turned out to have a very short half-life, and so in vivo, the enzymes were exposed to both configurations (one of which turned out to be toxic).

The enantiomeric equilibrium shown above for the benzolactam in fact qualifies as that for configurations, since both enantiomers can be isolated (their half-life is clearly > 1000s) and separately tested for recognition by enzymes.

How can I add any value to the above chemistry? Well, I decided to perform a search of the crystal structure database, and I added two geometric parameters;

1. The torsion about the 2-3 bond (1-2-3-4)
2. the torsion about the 3-5 bond (4-3-5-7).

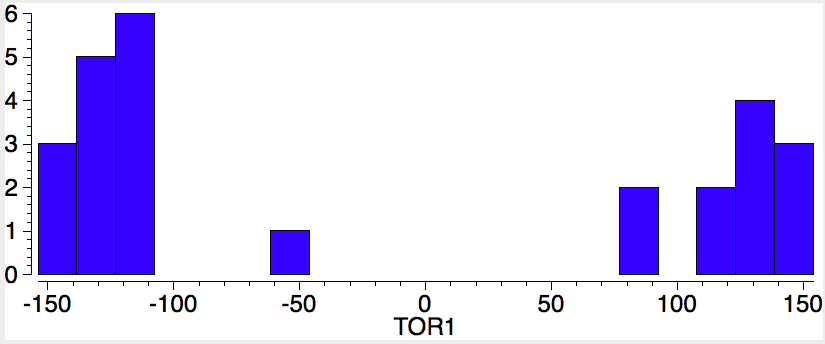
The sign of the first is critical, since the two possible atropisomers have opposite torsion angles. The value of the second relates to Pauling’s assertion that rotation about the amide bond is indeed restricted to two values, either 0 or 180°. So these two concisely blend atropisomerism and configuration. I start with a search of the above system using just the first torsion angle. It shows a nice clustering into those with strongly -ve and those with strongly +ve values; configurational atropisomers! Of course, it does not tell us what the barrier to interconvert them is; that has to be measured (or calculated) separately.

Next, I am showing a 2D map of both torsion angles. This shows again the first distribution, but reminds us that the torsion 4-3-5-6 stays resolutely at ~0 for all the compounds (the amide in other words is planar).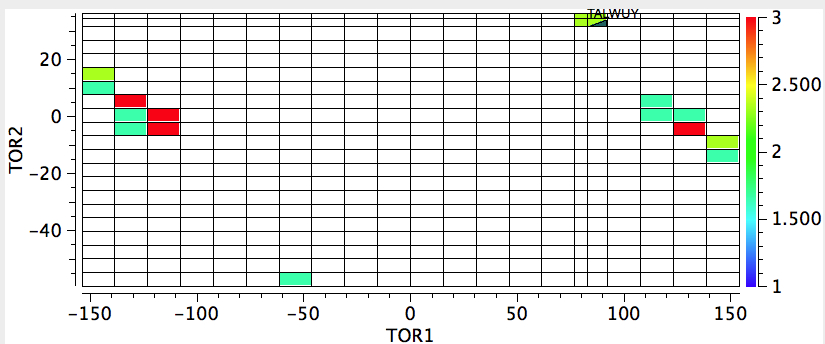 

Oh, a practical point. I mentioned a calculation could be done to estimate the barrier to enantiomerising the two atropisomers. This takes hours, and days if the transition state is awkward (and atropisomers can be so). But the above plots literally took perhaps 2 minutes each! Very cheap insight!

---

^‡Note the use of the word conformation in its title. It could equally validly be configuration! Which is better?

This entry was posted on Sunday, February 9th, 2014 at 10:25 am and is filed under General, Interesting chemistry. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.