I have posted often on the chemical phenomenon known as hypervalency, being careful to state that as defined it applies just to “octet excess” in main group elements. But what about the next valence shell, occurring in transition metals and known as the “18-electron rule”? You rarely hear the term hypervalency being applied to such molecules, defined presumably by the 18-electron valence shell count being exceeded. So the following molecule (drawn in three possible valence bond representations) first made in 1992 intrigues.[cite]10.1002/anie.199203231[/cite]
The molecule comprises six phosphinidene ligands (RP:, R=tert-butyl), the P analogues of nitrenes and arranged around nickel to form an unusual hexagonal planar coordinate species and with three of the t-butyl groups facing up and three down. This arrangement totally obscures the two nickel diaxial positions, preventing any ligand from occupying them. One may even speculate that the dispersion attractions between the two pairs of three t-butyl groups might be unusually stabilising,‡ maybe even on a par with those reported by Schreiner and co-workers for t-butyl substituted triphenylmethanes and noted on this blog.
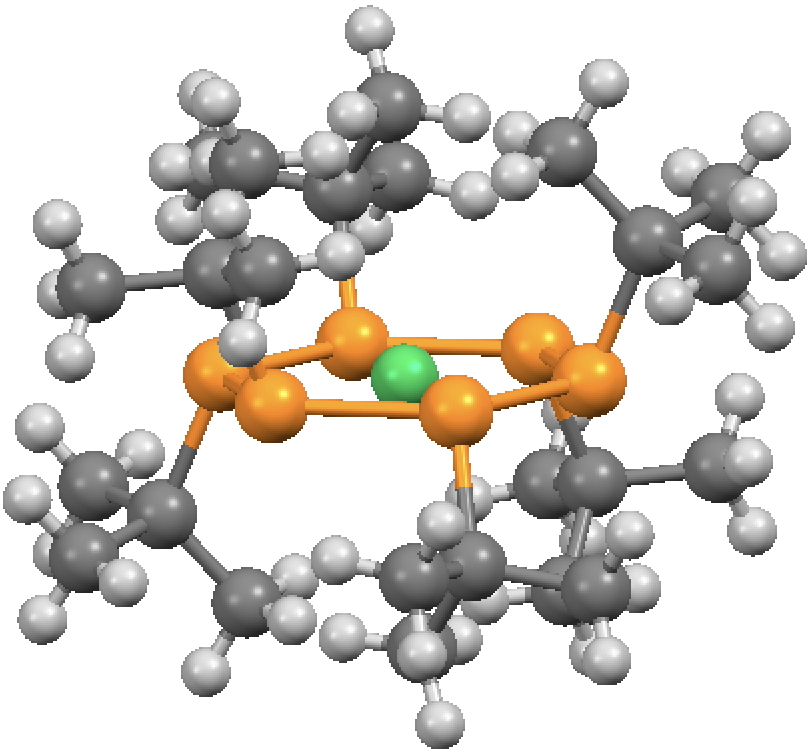
Nitrenes can be represented coordinating to a metal as RN=M. If the analogy extends to P, the valence bond structure 1 above would result and the six P atoms would contribute 12 electrons to the Ni valence shell. Since the Ni shell is [Ar].3d8.4s2 adding another 12 electrons would make 22 electrons, thus exceeding the 18-electron rule. In fact it was never suggested as such; in the 1992 analysis of the bonding[cite]10.1002/anie.199203231[/cite], the authors clearly state “The electronic structure … cannot be described in terms of the 18e rule”. To support this, they draw the structure in form 3 above, which implies a Ni valence shell of 16e, albeit also implying a Ni bond index of ~6.
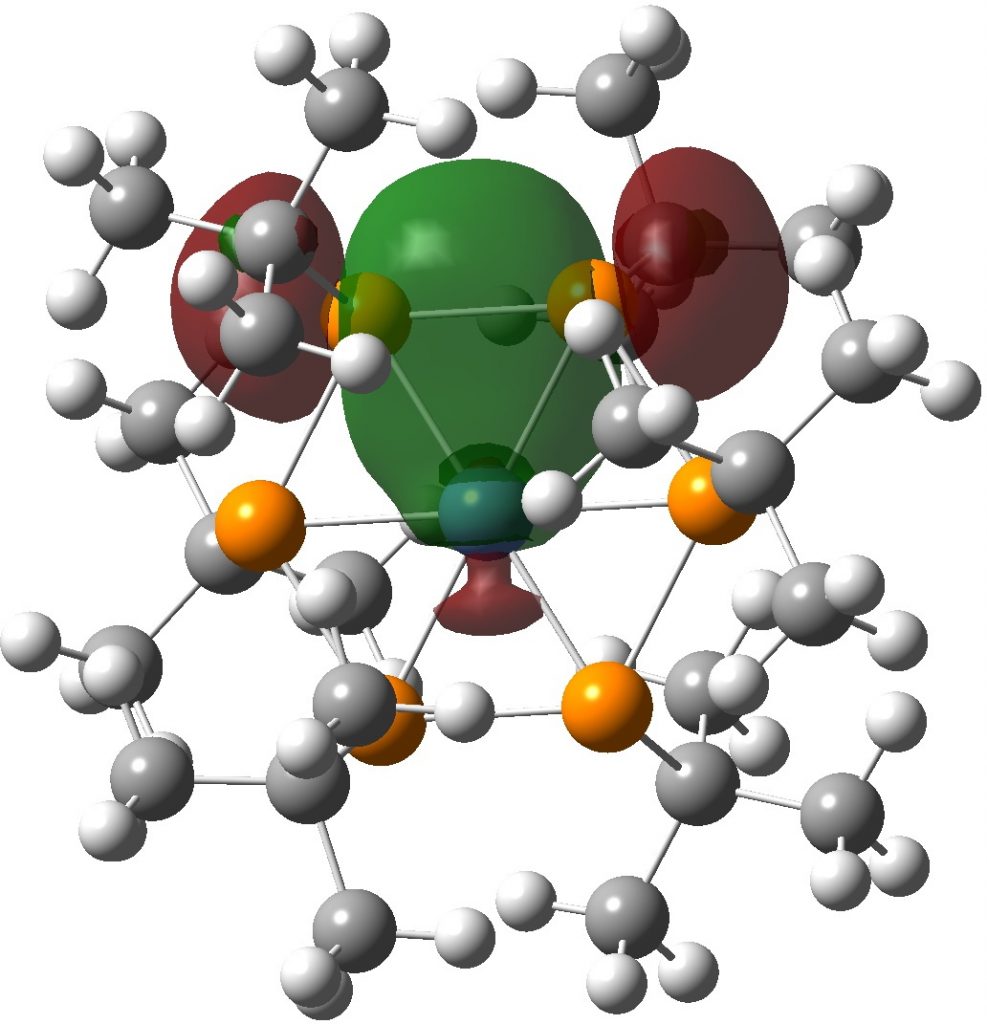
Time I thought for calculations (wB97XD/Def2-TZVPP).† The calculated NBO bond index at Ni is in fact 2.38 and the individual Ni-P bond orders are 0.37. The P bond indices are each 3.24 and the P-P bond orders are 0.88. The final electronic configuration is [Ar]3d9.53.4s0.22.4p0.64.4d0.01.5p0.01 and the natural charge on Ni is -0.39. I show one NBO orbital which illustrates the two-electron-three-centre interaction spanning two P atoms and the Ni and giving rise to the modest Ni-P bond order.
The Ni electronic structure of [Ar].3d8.4s2 normally corresponds to its divalency, so in this sense it is mildly hypervalent. Overall, representation 2 above is perhaps more accurate than 3. The ELF (Electron localisation function) of the electron density is shown below (t-butyl groups represented by a single carbon) with the ELF basins highlighted. Basin 2 is a P lone pair, with an integration close to 2e. Basin 1 is a P-P basin with an integration of 1.89 and finally 3 is indeed a P-Ni basin, but with an integration of only 0.06e.
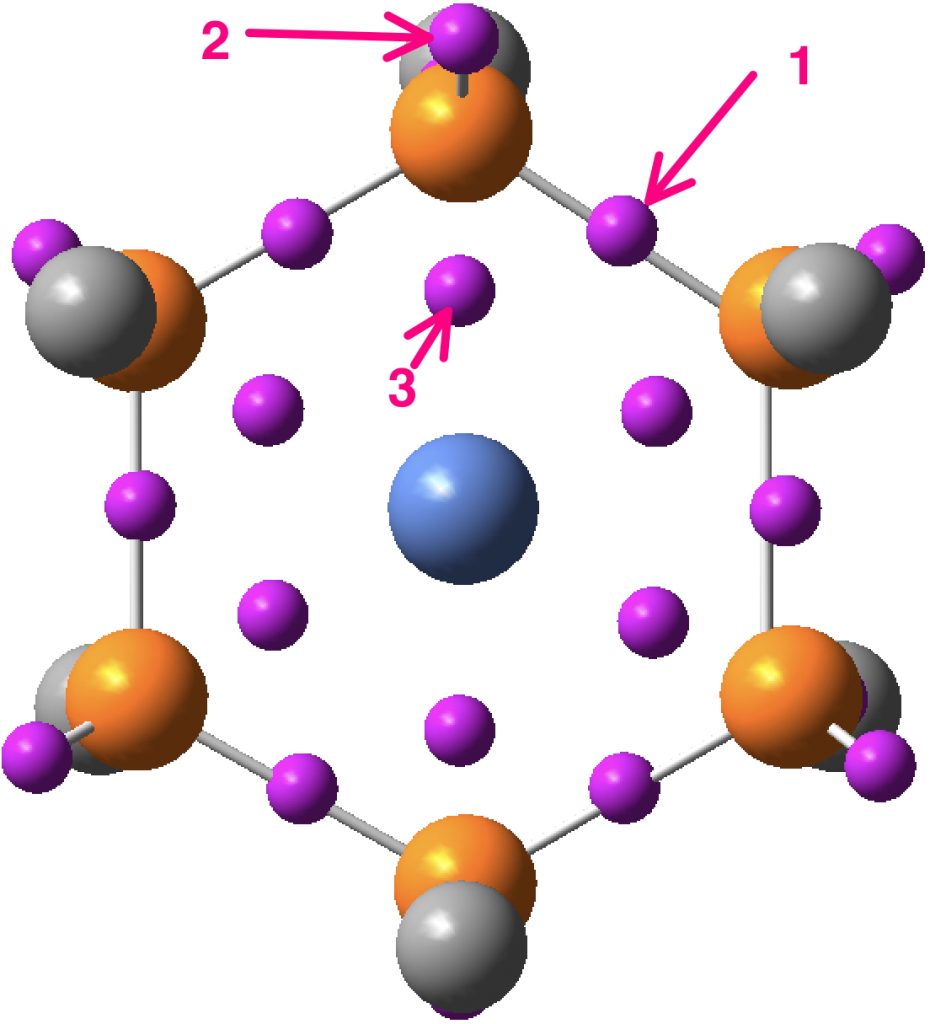
So this molecule really is a ring of six P atoms, encapsulating at its centre a lone Ni(II) atom. Rather than being hypervalent, perhaps it is most interesting as a complex in which a metal atom is contained in and perturbed by a dispersion-stabilized sphere of ligands.[cite]10.1021/acs.jctc.5b01100[/cite] We need more examples!
‡The original authors[cite]10.1002/anie.199203231[/cite] merely stated that electron correlation effects are decisive for the stability. Of course, dispersion attractions are indeed a form of electron correlation! †FAIR data doi: 10.14469/hpc/3925



I have added an NCI (non-covalent-interactions) analysis from two views, as per below. The green regions represent attractive dispersion interactions.
There’s a typo in structure 3 above, there seems to be an errant hydrogen atom attached to one of the phosphorus atoms. Trivia aside, this is a fascinating molecule. As this is essentially a ligand cage containing a Ni atom, one wonders what happens if Ni is replaced by its neighbours – Pd might not fit, but Co and Cu should.
Thanks for spotting the typo (Chemdraw has too much “AI” at times).
Yes, the molecule itself is fairly unique; only the As analogue is known.