One of the most fascinating and important articles dealing with curly arrows I have seen is that by Klein and Knizia on the topic of C-H bond activations using an iron catalyst.[1] These are so-called high spin systems with unpaired electrons and the mechanism of C-H activation involves both double headed (two electron) and fish-hook (single electron) movement. Here I focus on a specific type of reaction, the concerted proton-coupled-electron transfer or cPCET, as illustrated below. These sorts of reactions happen also to be of considerable biological importance, including e.g. the mechanism of photosynthesis and many other important transformations.
A hydrogen atom comprises a proton and one electron. The question is whether the proton and the electron travel together as a true hydrogen atom when the hydrogen relocates, or do they each take their separate way, as in the PCET reaction shown above. I will discuss the arrows shown briefly first.
- The blue arrow originates at an oxygen lone pair, donating two electrons into a O-H bond.
- The hydrogen starts off with two electrons in a C-H bond. In a pure proton transfer, it would lose both these electrons to the carbon (as an acid) and the proton would travel to the oxygen (as the base, which receives the proton). In fact these two C-H electrons go off in different directions.
- One (shown with a red fish-hook curly arrow) goes to the carbon to form a carbon radical.
- The other electron (shown with a dashed fish-hook curly arrow) travels to the Iron. The latter starts off in oxidation state +3 with five unpaired electrons in the high spin state (of which only one is shown above) and is reduced by receiving this electron to an oxidation state +2 and four unpaired electrons (again these are not shown above) with the fifth unpaired electron now becoming a carbon-centered radical.
- The formal charges on the atoms change. The oxygen shares its lone electron pair with a hydrogen and so formally looses its exclusive hold on that electron pair and becomes formally positive. The iron receiving an electron becomes less positive/more negative, changing from Fe(III) ≡ 3+ → Fe(II) ≡ 2+.
- In this representation, both the number of unpaired electrons and the charges balance on both sides of the equation, a crucial aspect of using curly arrows. One cannot create charge out of nothing. Similarly one cannot change the number of unpaired electrons on either side of the equation, unless the electronic state itself changes.
- Finally, note that the number of lone pairs in this instance also balance.
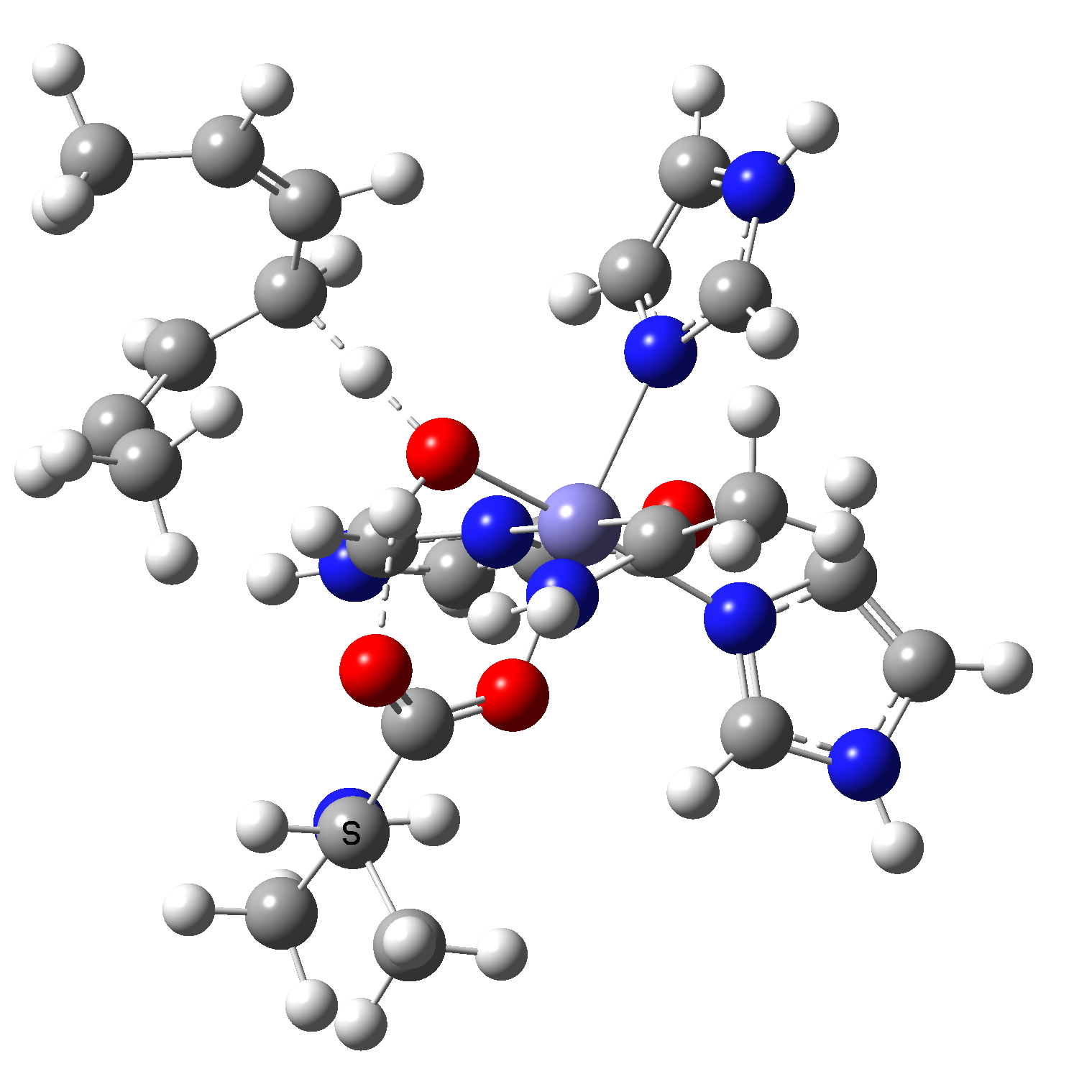
Now for an actual calculation of the reaction path using quantum mechanics.[1] The actual molecular model used is shown below. The C-H bond comes from a bis(allylic) alkene, whilst the ligands around the Fe include three neutral imidazole units coordinated through N, the methylalanine aminoacid anion is coordinated through one O(-), neutral acetamide is bound through O and hydroxyl anion (-) completing the octahedral coordination. The two ligand anionic charges noted are formally balanced by Fe(2+), and specifying that the whole system itself has a charge of (+) gives us an oxidation state of Fe(3+) with five formal valence electrons (down from 3d6.4s2 for the neutral atom). Only the hydroxyl ligand to Fe is shown above, the other five are hidden. The whole system is “high spin”, which means it has five unpaired electrons, only one of which is shown for the reactant Fe atom in the schematic diagram above. The other four unpaired and unshown electrons on the Fe are common to both reactant and product.
With the proton going in one direction, and an electron elsewhere, one might expect a change in the dipole moment properties. Below you can see the quite abrupt change in these properties in the same region that the electron/proton transfers happen.
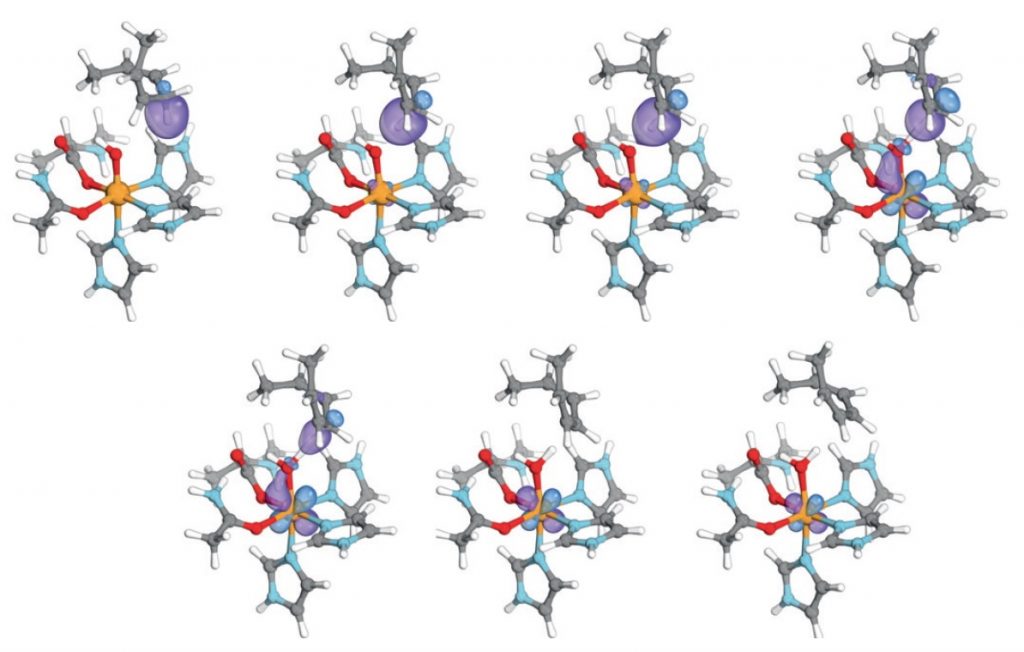
The progress of the reaction is shown by a set of specific types of localised orbital (actually called an IBO or intrinsic bond orbital in this instance) as the reaction evolves from the left to the right. You can think of some of these orbitals, selected on the basis of their changes in energy as the reaction proceeds, as corresponding to the curly arrows for the reaction. It is possible to reduce such orbitals to a point (a locus) by increasing their isosurface threshold and then to chart these locii as the reaction proceeds. This would then correspond to the path of a curly arrow.
Below is a specific orbital transformation, corresponding to the curly arrow shown at the top here in dashed red.[1] This orbital starts off located along the C-H bond and as the electron transfers, the orbital morphs (abruptly, like the dipole moment properties above) into an d-orbital located on the iron. It vanishes from one region and re-appears in another, a little like the famous cheshire cat.
When I gave my talk to students alluded to in an earlier post, I was keen to get the message over that the veritable concept of curly arrows, which will be 100 years old in 2024, is still an evolving and modern concept and not stuck in any ancient time warp. This mechanism by Klein and Knizia illustrates nicely how true that is. The take home message is that curly arrows really are fit for the 21st century.
References
- J.E.M.N. Klein, and G. Knizia, "cPCET versus HAT: A Direct Theoretical Method for Distinguishing X–H Bond‐Activation Mechanisms", Angewandte Chemie International Edition, vol. 57, pp. 11913-11917, 2018. https://doi.org/10.1002/anie.201805511