< cover | measures | overlap | rotation | csm | ccm | bibliography >

Kelvin.

Abstract: Qualitative measurements of chirality are based on the assignment of left/right handedness to particular structures. This system is of limited use if a quantitative measurement is required – either relative to the molecule’s enantiomeric pair or to a specified symmetry group. There has been great deal of interest in recent years concerning useful measures of symmetry and chirality and the comparison of these with the molecule’s physical, and in particular, pharmaceutical properties. This review is designed to give an overview of these measure.- concentrating in particular on that of Continuous Symmetry Measurement (CSM).

Objects can be classified and collected into groups with respect to the symmetry elements that they share. Such classifications are commonly used as an extremely powerful tool for discussing their physical properties⁽¹⁾. Perhaps more importantly, the grouping of molecules by their basic symmetrical shape allows the comparison of properties within groups, possibly revealing trends that would otherwise remain hidden.

Unfortunately molecules are rarely perfectly symmetrical, and as a result, grouping them by resemblance to idealised symmetries is both rather crude and likely to miss some of the subtler aspects of the molecule’s shape. In particular, it would be nice to able to compare the shapes of two significantly dissimilar asymmetrical molecules and hence gain ideas as to the relationships between any shared properties and any similarity in their shape. As an example, we might ask:

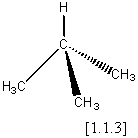
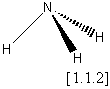
Obviously the methane has the greater ‘amount’ of tetrahedral symmetry, but how much greater? And how will it affect say, their infra-red spectra? In addition, what happens if we substitute isobutane [1.1.3] for methane (more ‘ammonia like’)? How about a mono-deuterated methane? From a purely classical viewpoint, we should not ask such questions. Objects are either symmetrical or not and the description is either black and white with no shades of grey. Classically methane is Td, with ammonia and isobutane being C_3n . However all three are roughly similar in shape and so might be expected to share some properties. We can see that this classical approach is too limiting to allow the comparison of different symmetry groups or the quantitative relation of symmetry to property trends.

We need to find some technique for directly measuring symmetry – either relative to another object or with respect to the nearest symmetry group. A wide range of possible solutions have been proposed over the last twenty years. As a result, there is a large number of potential measures, with wildly different approaches and advantages/disadvantages. This review is intended to give a general overview of this subject and to compare and contrast some of these approaches.

An important subset of this general requirement for a symmetry measurement is the need to quantify the chirality of a molecule. A chiral molecule can not be superimposed onto its mirror image by any number of translational or rotational operations.^(2,3) This means that a chiral molecule and its mirror image must be considered to be two separate but linked species – a enantiomeric pair.

Again, by the classical definition molecules either have left or right handed chirality or are achiral. This thinking was developed from early crystal shape and plane light rotation studies which implied that chirality was a property that a molecule either had or had not, in a similar fashion to symmetry (although even more restrictive).

As explained earlier, such a system does not allow the comparison of different types of chiral molecule. This is a serious problem. A pair of enantiomers will have essentially identical physical and chemical effects in a non chiral environment (polarised light can be seen as chiral). But this is decidedly not the case in a biological system. ⁽⁴⁾

Most biological molecules are in themselves chiral and may have particularly complex shapes. In addition, many proteins and enzymes are evolved to interact very specifically with a particularly shaped substrate. If an enzyme has a reaction site shaped for maximum interaction with one enantiomer of a chiral molecule it is rather unlikely to interact to the same extent (if at all) with the other. More worryingly, another unrelated enzyme may bind instead and if the chiral molecule is a drug this could have unexpectedly toxic side effects. In vivo properties of a pair of enantiomers can be very different and they may well have differing pharmacology and toxicology. A simple example illustrates this important point; D-glucose is sweet whilst L-glucose has no taste.⁽⁵⁾ More seriously, the L isomer of thalidomide was found to be an effective tranquilliser but there is evidence that D isomer impurities were responsible for the resulting birth defects. Therefore from a medical point of view, different enantiomers must be considered separate species and a racemic drug is generally regarded as 50% impure.^(3,6)

This indicates the importance of chiral analysis in drug design and the need for better understanding of chiral recognition in biological systems. It has been suggested that a quantitative measure of chirality would allow the identification of possibly dangerous enantiomers. The greater the chiral difference between an enantiomeric pair, the more likely that they will have different biological effects (absorption, biotransformation, excretion etc.)⁽⁷⁾ A system of chirality measurement could also be related to efficiency of various separation techniques, for example HPLC. Such a relationship might allow the prediction of the best techniques / conditions to allow maximum separation of the two enantiomers.

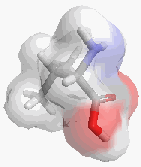
Recently a number of systems have been postulated which allow chirality measurement in a manner equivalent to that just discussed. It should be noted that chirality is a property dependent on the perceived symmetry of a molecule, as well as the resolution of the ‘probe’ being used. A large probe won’t notice the smaller changes in the molecules structure, hence an enzyme with a large, poorly defined binding site will be less likely to distinguish between enantiomers than one with a small, very specific binding site. In [1.2.1] the top shape is less chiral than the bottom due to the lower probe resolution.

It must be decided which of the standard molecular models the measurement should be based on. This will depend on the properties we are interested in and it isn’t really feasible to base the chirality measurement on more than one property. Useful properties include: the molecule’s skeletal structure, van der Waals’ surfaces, volume, mass, electronic isodensity surfaces, MEP isosurfaces, electron orbital shapes and many more.

We must also decide if vibrations, complex folding or fluxionality should be taken into account. If they are, the measure may become much more complicated. Generally systems are considered as time or aggregate averaged or to be in some equilibrium state. This reduces the number of calculations required but may obviously lead to reduced accuracy.

The use of group theory allows the systemic analysis of symmetry and therefore is the foundation for many symmetry/chirality measurement methods. The theory is based on the identification of general sets of symmetry operations which, when carried out on an object will leave it looking exactly the same. Such operations include; rotations about axes, reflections across planes and inversions through a single point. For each operation, there is a related symmetry element – this refers to the axis, plane or point about which the operation is carried out.⁽¹⁾

If an object looks the same under a particular operation, then it is said to own the symmetry element related to that operation. Certain combinations of elements are common and these are then collected together as symmetry groups that are descriptive of a certain shape (all groups are closed). By identifying which elements an symmetrical object owns it can be assigned to a symmetry group. This group is then used as a convenient label. List of symmetry groups and the elements they contain can be found in the literature.⁽¹⁾

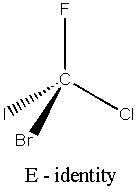
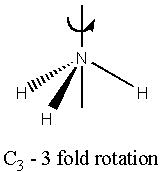
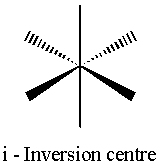
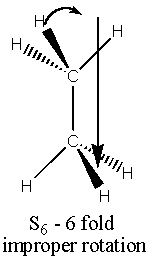
There are five main types of symmetry operations (and hence 5 types of element – see the diagrams)^(1,8);

C_n n fold rotation about the principle axis

i Inversion

Hence the symmetry group D_3h (trigonal) contains the elements E, C₃, 3 C₂, and s _h . This system also suggest methods by which certain symmetry groups can be said to have the character of other groups, depending on their shared elements. Extending this to asymmetrical molecules, consider the replacement of the two of the hydrogen atoms in methane by deuterium. This completely changes the classical symmetry of the molecule (Td to C_2v). However it is still ‘nearly tetrahedral’ and as such, will still have a large amount of Td character. The aim of chirality measurement is to put a quantitative value to this amount.

This notation allows the easy identification of chiral and achiral molecules. In order for a structure to be achiral it must possess either a reflection plane (s = S₁), a centre of inversion (i = S₂) or higher order improper rotation axes S_2n. In practice the most important from a molecular point of view is the s mirror plane. This immediately suggests an approach for measuring chirality, since for every chiral enantiomeric pair there must be a series of achiral molecules that are very similar in structure but which do have an S_2n symmetry element. If the achiral structure most similar to the enantiomers can be found, it can then be used as a starting point. The chirality measure would then be the difference between the chiral molecule and its closest achiral relative.

Crystal Field splitting of d electron levels in a transition metal complex is well understood. The amount and pattern of this splitting depends on the symmetry of the ligands around the complex. A Td crystal field will act to split the normally degenerate 5 d orbitals into a high triply degenerate t₂ level and a low doubly degenerate e level. By contrast the octahedral (Oct) crystal field gives the reverse splitting. These effects are due to the repulsive interaction of the d electron orbitals on the metal with the s and p orbitals on the ligands.⁽⁹⁾

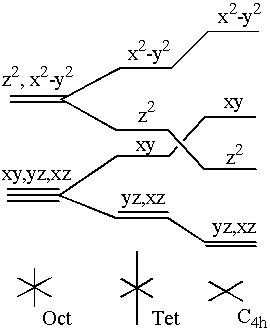
This sort of splitting becomes relevant when we consider what will happen in the case of a tetragonally (Tet) distorted octahedron, where the z axis has been extended and the x and y axes have been compressed respectively. The tetragonally distorted system is normally considered to have a splitting pattern half way between the octahedral starting case and the planar (C_4h) concluding situation (where the z ligands no longer exist). In other word it can be considered to have a symmetry effect that is a mixture of the Oct and C_4h effects. By measuring the amount of each symmetry group in the tetragonal case we could then relate this to the amount of shift in the energy levels and resulting changes in the complex’s electronic spectrum. A similar situation occurs in the splitting of degenerate p orbitals. Hence a symmetry measure would help give a better understanding of these physical effects.

--> next

< cover | measures | overlap | rotation | csm | ccm | bibliography >