Chapter 3 Dynamic Chirality
<
cover
| measures
| overlap
| rotation
| csm
| ccm
| bibliography
>
A rather unusual scale for the quantitative assessment of chirality has been proposed. It is based on the rotational properties of shapes in two dimensions. This measure is restrictive but may prove to be a useful tool for surface chemistry.
3.1 Absorbed Molecules
The reduction of dimensionality from three to two acts to significantly relax the required conditions for chirality. As a direct result, the properties of a chiral shape in two dimensions are simpler than for an object in three.
As was pointed out by Hel-Or, Peleg and Avnir,(15,16) molecular chirality must therefore be ‘far more common in the absorbed state compared to the bulk state.’ This can be illustrated by considering the change the achiral trans-2-butene undergoes on absorption to a surface [3.1.1];
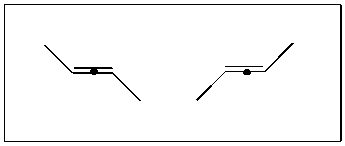 [3.1.1] Formation of a racemic mixture of chiral species as trans-2-butene is absorbed onto a planar surface.
[3.1.1] Formation of a racemic mixture of chiral species as trans-2-butene is absorbed onto a planar surface.
The two species can not be superimposed since rotation (or translation) in the third dimension is now constrained. In general, a planar molecule is chiral under 2D conditions if it does not have a symmetry axis in the 2D plane (greater than C1 of course - compare with the similar Sn requirements for three dimensional chirality). Hence cis-2-butene will not be chiral on absorption. It might be expected that absorption chirality would be represented in the products of any reaction involving molecule to surface interactions. This effect is well documented in the case of a chiral sp2 to sp3 conversion at the surface of a catalyst.(28)
Consider the absorption of a tetrahedral carbon centre to a planar surface. Relaxation of the conditions for chirality occur and the bound compound will form a racemic mixture. An interesting situation arises if the catalytic surface also happens to be chiral (for example the surface of a chiral crystal). In this case you might expect the surface to be able to distinguish between the two enantiomers and a stereoselective reaction to occur. Exactly this is seen when using chromatography to separate enantiomers (for example by chiral HPLC).
Any moving object may also be considered to have chirality even if the stationary object does not. Relating this back to our surface absorbed molecules, we can see that if a molecule is able to rotate about any arbitrary axis (perpendicular to the surface) then it can be considered to have rotational chirality, irrespective of any stationary 2D chirality. Hence the left and right rotating versions of the molecule are known as dynamic enantiomers.
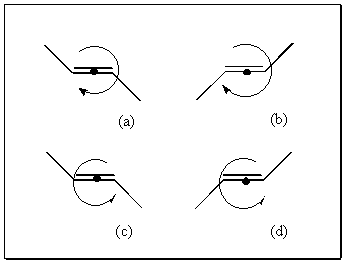
An example of this is ethyne, which will absorb to and rotate on the surface of crystalline E-stylbene. In principle, the two rotation directions and hence the two dynamic enantiomers should have differing activation energies. If the molecule has surface chirality of its own then there is the possibility of four different species grouped into two pairs of dynamical enantiomers (a,d and b,c in [3.1.3])
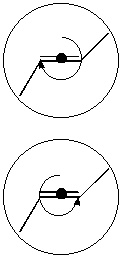
3.2 Rotational Chirality
Hel-Or, Peleg and Avnir used these concepts of surface chirality and rotation about an axis to propose a dynamic approach to measuring the chirality of an absorbed molecule. This measured the intensities of some rotational property of a molecule and then compared the results when rotating that molecule in the opposite direction. Identical intensities will be measured if the molecule is achiral but they will be different if the molecule is chiral. The two enantiomers of a chiral molecule will show the same difference but with an opposite sign.
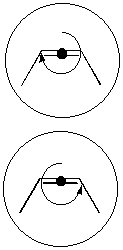
The easiest way to visualise this is to consider the molecule as a rigid structure rotating in some mobile medium - say a bed of sand. The molecule may be 2D achiral or it may be one of two chiral enantiomers. The chirality measure will be defined as the difference in the quantity of sand collected by the structure under a complete rotation of 360o in both clockwise and counter-clockwise directions. There are two possible results:
a) The molecule is 2D achiral and therefore will collect the same amount of sand in both directions. The difference in the amount of sand collected is zero and S(rot) = 0
b) The molecule is 2D chiral and the amount of sand collected is not the same in both directions, the difference is non zero and equal to S(rot). The enantiomer will also collect the same amounts of sand but by rotating in the opposite directions, hence will yield an S(rot) value with the opposite sign (fairly irrelevant).
These situations can be seen in [3.1.4] and [3.1.5]. In the first case, cis-2-butene is achiral in 2D, so rotations in either direction will collect the same amount of sand. This is not the case with trans-2-butene, where one rotation direction will collect less sand than the other (since the shape of the molecule will ‘push’ the sand out of the way rather than collecting it). Effectively this method works by measuring the length of the molecular backbone that ‘collects’ sand under each direction of rotation.
Hel-Or’s proposed measure was based on a computerised image analysis technique. The molecule is represented as a line presentation, with K being the set of all the pixels in that presentation. Similar methods could be derived based on other types of molecular model.
Let ![]() be the ordered set of edge pixels of K, (E Í
K)†. These pixels are counted by following the circumference of the object so that it is always to the right of the pixel line. This means that each pixel in a open line drawing will be counted twice but closed rings can then be taken into account. For each boundary pixel (ei) for a molecule rotating around a centre origin O, the following are defined:
be the ordered set of edge pixels of K, (E Í
K)†. These pixels are counted by following the circumference of the object so that it is always to the right of the pixel line. This means that each pixel in a open line drawing will be counted twice but closed rings can then be taken into account. For each boundary pixel (ei) for a molecule rotating around a centre origin O, the following are defined:
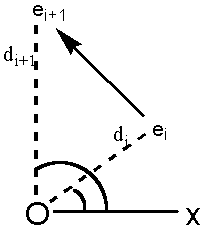
- ri: the vector from O to ei
- di: the length of ri
- q i: the angle between ri and the x-axis (-p < q i < p )
- D di = di+1 – di
- D q i = q i+1 – q i (equal to the angle [ei, 0, ei+1] where (-p < D q i < p ))
A boundary segment between ei and ei+1 will encounter particles only if:
D di > 0 for counter-clockwise rotations,
D di < 0 for clockwise rotations,
Any encountered particles will only be collected if D q i > 0 – otherwise they will be thrown off by ‘centrifugal force’. Defining the subsets r and l so that r is the set of boundary pixels that collects particles on clockwise rotation and l on counter-clockwise rotation (r, l Ì E remembering E Í K):
![]()
![]() ‡
‡
Of course: r Ç
l = 0 and r È
l Î
K and in practice thresholds are chosen in preference to 0 since the signs of D
q
i and D
di are rather unstable around zero. The normalised difference of these subsets is then used as the chirality measurement, where ![]() is the number of members in set E etc.:
is the number of members in set E etc.:
![]()
This chirality term is known to have the following properties;
1) If ![]() then S(rot) = 0. This can occur even if the molecule is chiral and is a problem solved by the refined measure.
then S(rot) = 0. This can occur even if the molecule is chiral and is a problem solved by the refined measure.
2) The degree of chirality increases directly with S(rot).
3) S(rot) > 0 implies left handed chirality (more particles collected under counter-clockwise turn) and S(rot) > 0 implies right handed chirality.
Further refinement uses the concept of torque (force times distance, from the axis of rotation) and defines:
![]()
![]()
letting dmax be normalised to avoid problems with scaling. This system is analogous to calculating the torque applied on the central axis by the particles when rotating in either direction. The measure is now the normalised difference between these torques;
![]()
Now if R(rot)’ = 0 the object can confirmed as chiral. It should be noted that these measures both depend on the choice of the axis of rotation. By analogy to the property overlap measure, the axis must be chosen so as to give the largest chirality measure. Again, locating this axis is likely to be the most computationally intense part of the measurement.
Hel-Or et al. demonstrated that this rotational chirality measurement can be used to investigate the properties of alkane series. It was found that in a series of all trans-n-alkanes, odd numbered carbon skeletons are not chiral in 2D (propane, pentane, heptane etc.) Even numbers are chiral (butane, hexane, octane etc.) It was also noticed that the amount of chirality decreases with increasing n. Since the difference between the odd and even alkanes is one methylene group, the relative chiral effect of this group will decrease with increasing n. Hence we would expect the value of S(rot)’ to fall.
In conclusion, if an object is rotated in a viscous medium, then the force exerted on that object upon clockwise rotation will only be the same as that exerted on counter-clockwise rotation if the object is achiral. If the object is chiral then the difference between these forces can be used as a measure of that chirality. This measure, whilst easy to calculate is very specific to 2D systems and is therefore of limited use. The continuous symmetry approach proposed by the same group is much more general.
--> next
<
cover
| measures
| overlap
| rotation
| csm
| ccm
| bibliography
>